Σε ένα υποθετικό πηγάδι που διέρχεται από το κέντρο της Γης και συνδέει δυο αντιδιαμετρικά της σημεία, αφήνουμε να πέσει ελεύθερα ένα σώμα. Σε πόσο χρόνο το σώμα θα φθάσει στο άλλο άκρο του πηγαδιού;
Αν υποθέσουμε ότι η μάζα της Γης είναι ομοιόμορφα κατανεμημένη σε έναν τέλεια σφαιρικό όγκο (σταθερή πυκνότητα) και ότι δεν υπάρχει αντίσταση του αέρα, τότε το πρόβλημα μπορεί να απαντηθεί εύκολα, χρησιμοποιώντας τον νόμο του Gauss για το βαρυτικό πεδίο της Γης ή που είναι το ίδιο, χρησιμοποιώντας τον νόμο της παγκόσμιας έλξης, με κάποια απλά επιχειρήματα συμμετρίας.
Εκ πρώτης όψεως φαίνεται πως απαιτείται αρκετός χρόνος, εφόσον το σώμα που πέφτει στη σήραγγα πρέπει να διανύσει μια απόσταση ίση με τη διάμετρο της Γης – 12.800 km περίπου. Αλλά τι εννοούμε όταν λέμε αρκετός χρόνος; ένα έτος; κάποιοι μήνες; μερικές μέρες; λίγες ώρες; ή αρκετά λεπτά της ώρας;
Θα μπορούσαμε να πάρουμε πολύ γρήγορα μια χονδρική εκτίμηση του χρόνου αυτού, χωρίς την χρήση των νόμων της φυσικής, διαμέσου της μεθόδου της διαστατικής ανάλυσης.
Διαστατική ανάλυση
Ο χρόνος πτώσης σε πεδίο βαρύτητας ως γνωστόν δεν εξαρτάται από την μάζα  του σώματος που πέφτει. Εξαρτάται, όμως από την μάζα της Γης
του σώματος που πέφτει. Εξαρτάται, όμως από την μάζα της Γης  που δημιουργεί το βαρυτικό πεδίο. Περιμένουμε επίσης να εξαρτάται από την ακτίνα της Γης
που δημιουργεί το βαρυτικό πεδίο. Περιμένουμε επίσης να εξαρτάται από την ακτίνα της Γης  , καθώς επίσης και ότι στην τελική εξίσωση θα περιέχεται η σταθερά της παγκόσμιας έλξης
, καθώς επίσης και ότι στην τελική εξίσωση θα περιέχεται η σταθερά της παγκόσμιας έλξης  .
.
Με λίγα λόγια ο ζητούμενος χρόνος θα υπολογίζεται από μια σχέση της μορφής:

Οι μονάδες μέτρησης του πρώτου μέλους θα πρέπει να είναι ίδιες με τις μονάδες μέτρησης του δεύτερου μέλους.
Οι μονάδες μέτρησης του πρώτου μέλους θα πρέπει να είναι ίδιες με τις μονάδες μέτρησης του δεύτερου μέλους.
Έτσι, αντικαθιστώντας τις μονάδες των μεγεθών που περιέχονται στην παραπάνω σχέση προκύπτει η εξίσωση:
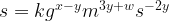
η οποία ικανοποιείται μόνο όταν
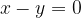 ,
,  και
και 
ή όταν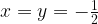 και
και 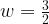 .
.
η οποία ικανοποιείται μόνο όταν
ή όταν
Συνεπώς μια εκτίμηση για τον χρόνο που χρειάζεται ένα σώμα για να διασχίσει μια σήραγγα που διέρχεται από το κέντρο της Γης, πέφτοντας ελεύθερα μόνο υπό την επίδραση του πεδίου βαρύτητας, θα δίνεται από την σχέση

Σε ανάλογη σχέση καταλήξαμε εφαρμόζοντας την ίδια συλλογιστική στην ανάρτηση με τίτλο “Σε πόσο χρόνο θα κατέρρεε βαρυτικά ο Ήλιος αν ξαφνικά σταματούσαν οι πυρηνικές αντιδράσεις στο εσωτερικό του;“
Αν θέσουμε τις τιμές της σταθεράς της παγκόσμιας έλξης, της ακτίνας και της μάζας της Γης – που εύκολα βρίσκει κανείς στο google –, προκύπτει ότι

Υποθέτοντας ότι η Γη έχει σταθερή πυκνότητα
Λύνοντας το πρόβλημα με τον κανονικό τρόπο αποδεικνύεται πως όταν μάζα βρίσκεται σε μια απόσταση  από το κέντρο της Γης, τότε η βαρυτική δύναμη που δέχεται είναι
από το κέντρο της Γης, τότε η βαρυτική δύναμη που δέχεται είναι
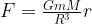
Aυτό σημαίνει ότι το σώμα εκτελεί απλή αρμονική ταλάντωση με σταθερή επαναφοράς

και περίοδο

Επομένως ο χρόνος για να φτάσει το σώμα από το ένα άκρο του τούνελ στο άλλο θα είναι

και περίοδο
Επομένως ο χρόνος για να φτάσει το σώμα από το ένα άκρο του τούνελ στο άλλο θα είναι
Καταρχήν παρατηρούμε ότι η σχέση που υπολογίσαμε χρησιμοποιώντας την διαστατική ανάλυση δίνει την σωστή τάξη μεγέθους και διαφέρει από την ακριβή εξίσωση μόνο κατά τον αριθμητικό παράγοντα π=3,14. Όμως, αυτό ήταν αναμενόμενο, διότι η διαστατικήανάλυση αδυνατεί να προσδιορίσει τις αδιάστατες αριθμητικές σταθερές.
Υποθέτοντας ότι η επιτάχυνση της βαρύτητας είναι σταθερή
Αν υποθέσουμε ότι η ένταση του πεδίου βαρύτητας στο εσωτερικό της Γης είναι σταθερή και ίση με την τιμή που έχει στην επιφάνεια της Γης 
τότε θεωρώντας ότι το σώμα εκτελεί ομαλά επιταχυνόμενη κίνηση, ο χρόνος κίνησης από το ένα άκρο της σήραγγας μέχρι το άλλο θα είναι

τότε θεωρώντας ότι το σώμα εκτελεί ομαλά επιταχυνόμενη κίνηση, ο χρόνος κίνησης από το ένα άκρο της σήραγγας μέχρι το άλλο θα είναι
Σταθερή πυκνότητα ή σταθερή επιτάχυνση;
Στην πραγματικότητα όμως, ούτε η πυκνότητα της Γης είναι ομοιόμορφη – σύμφωνα με την υπόθεση της σταθερής πυκνότητας υπολογίστηκε ο χρόνος των 42 λεπτών – ούτε βέβαια υπόθεση ότι της σταθερής έντασης του πεδίου βαρύτητας στο εσωτερικό της Γης ισχύει – βάσει της οποίας υπολογίζεται ο χρόνος των 38 λεπτών.
Ποιος από τους δυο χρόνους είναι ο πιο ρεαλιστικός; Όσοι επιλέγουν τον χρόνο που προκύπτει υποθέτοντας ότι η Γη έχει σταθερή πυκνότητα (42 min) κάνουν λάθος!
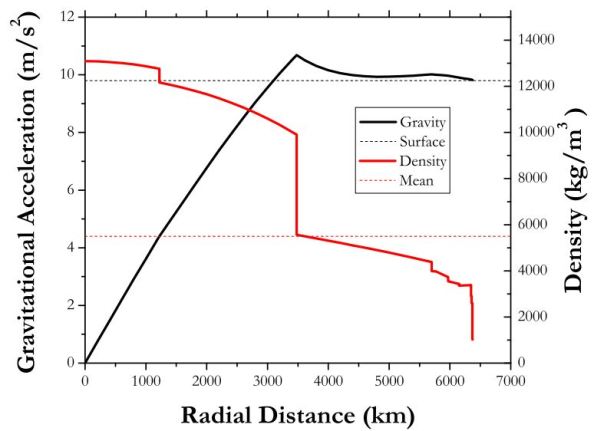
Η ένταση του βαρυτικού πεδίου (μαύρο χρώμα) και η πυκνότητα (κόκκινο) στο εσωτερικό της Γης συναρτήσει της απόστασης από το κέντρο της Γης σύμφωνα με το Preliminary Earth Reference Model (PREM)
To παραπάνω διάγραμμα μας δείχνει πως μεταβάλλεται η πυκνότητα της Γης συναρτήσει της απόστασης από το κέντρο της, σύμφωνα με το μοντέλο PREM.
Οι αριθμητικοί υπολογισμοί του Alexander R. Klotz, στην εργασία του με τίτλο “The Gravity Tunnel in a Non-Uniform Earth” που λαμβάνουν υπόψη την ρεαλιστική πυκνότητα της Γης δείχνουν ότι ο χρόνος που απαιτείται για να διασχίσει ένα σώμα το τούνελ που διέρχεται από το κέντρο της Γης είναι 38 λεπτά και 11 δευτερόλεπτα.
Οι αριθμητικοί υπολογισμοί του Alexander R. Klotz, στην εργασία του με τίτλο “The Gravity Tunnel in a Non-Uniform Earth” που λαμβάνουν υπόψη την ρεαλιστική πυκνότητα της Γης δείχνουν ότι ο χρόνος που απαιτείται για να διασχίσει ένα σώμα το τούνελ που διέρχεται από το κέντρο της Γης είναι 38 λεπτά και 11 δευτερόλεπτα.
Συμπερασματικά,
αν ανοίξουμε μια σήραγγα στη Γη που θα περνάει από το κέντρο της και θα φτάνει στην άλλη πλευρά της και στη συνέχεια αφήσουμε μια πέτρα να πέσει μέσα, τότε
η πέτρα θα φτάσει στο άλλο άκρο της σήραγγας σε χρόνο λιγότερο της μιας ώρας.
Για την ακρίβεια,
αν λύσουμε το πρόβλημα ως συνήθως, θεωρώντας την πυκνότητα της Γης σταθερή, τότε βρίσκουμε ότι η πέτρα φτάνει στο άλλο άκρο, εκτελώντας απλή αρμονική ταλάντωση, μετά από 42 λεπτά και 12 δευτερόλεπτα,
ενώ οι αριθμητικοί υπολογισμοί που παίρνουν υπόψη τους την πραγματική κατανομή της μάζας στο εσωτερικό της Γης, δίνουν χρόνο 38 λεπτά και 11 δευτερόλεπτα.
Αν λύσουμε το πρόβλημα θεωρώντας την χοντροκομμένη υπόθεση ότι το σώμα εκτελεί κίνηση με σταθερή επιτάχυνση και ίση με την επιτάχυνση της βαρύτητας στην επιφάνεια της Γης, τότε βρίσκουμε ότι η πέτρα φτάνει στο άλλο άκρο μετά από 38 λεπτά και 0 δευτερόλεπτα,
μια τιμή που διαφέρει μόνο 11 δευτερόλεπτα από την ρεαλιστικότερη προσέγγιση του προβλήματος!
αν ανοίξουμε μια σήραγγα στη Γη που θα περνάει από το κέντρο της και θα φτάνει στην άλλη πλευρά της και στη συνέχεια αφήσουμε μια πέτρα να πέσει μέσα, τότε
η πέτρα θα φτάσει στο άλλο άκρο της σήραγγας σε χρόνο λιγότερο της μιας ώρας.
Για την ακρίβεια,
αν λύσουμε το πρόβλημα ως συνήθως, θεωρώντας την πυκνότητα της Γης σταθερή, τότε βρίσκουμε ότι η πέτρα φτάνει στο άλλο άκρο, εκτελώντας απλή αρμονική ταλάντωση, μετά από 42 λεπτά και 12 δευτερόλεπτα,
ενώ οι αριθμητικοί υπολογισμοί που παίρνουν υπόψη τους την πραγματική κατανομή της μάζας στο εσωτερικό της Γης, δίνουν χρόνο 38 λεπτά και 11 δευτερόλεπτα.
Αν λύσουμε το πρόβλημα θεωρώντας την χοντροκομμένη υπόθεση ότι το σώμα εκτελεί κίνηση με σταθερή επιτάχυνση και ίση με την επιτάχυνση της βαρύτητας στην επιφάνεια της Γης, τότε βρίσκουμε ότι η πέτρα φτάνει στο άλλο άκρο μετά από 38 λεπτά και 0 δευτερόλεπτα,
μια τιμή που διαφέρει μόνο 11 δευτερόλεπτα από την ρεαλιστικότερη προσέγγιση του προβλήματος!

